线性回归（Linear Regression） 是利用线性回归方程的最小平方函数对一个或多个自变量和因变量之间的关系进行建模的一种回归分析。这种函数是一个或多个回归系数的模型参数的线性组合，只有一个自变量（自变量x和因变量y）的情况称为 一元回归，也称简单回归，大于一个自变量情况的叫作 多元回归。

它是一种历史非常悠久、应用非常广泛的统计模型，其核心是线性模型，主要思想是通过调整参数，使得所作直线尽可能拟合各个数据集点。

线性回归是最简单的机器学习模型，相当于机器学习的中的 ”Hello World“。

1. 一元线性回归分析

$\hat{y} = w^Tx_i + b$

上面的公式（1-1）是一个线性方程。

$w^Tx_i$ 是代表求两个向量的 内积（Dot Product），即按位相乘然后再求和，譬如两个向量 [1,3,5] 和 [2,4,6] ，求内积运算过程为：[1,3,5]T[2,4,6]=1×2+3×4+5×6=2+12+30=44

线性回归模型是用线性方程进行预测。按前面的约定，我们把机器学习模型的假设函数用符号H来表示，线性回归的假设函数就是线性函数，可以写成如下形式：

$H(x) = w^Tx_i + b$

给预测函数输入数据，也就是给式中的x赋值，预测函数经过计算后就能够返回一个结果，这就是预测值 $\hat{y}$

1.1. 损失函数的数学表达式解析

线性回归的损失函数选择使用 L2范数 来度量偏差，数学表达式如下： $L(x) = ||\hat{y} -y||^2_2$

公式（1-3）中有像一对双竖线的符号，还带下标。 $||\ ||_n$ 是范数符号，阿拉伯数字是n就代表Ln范数，这里下标是2，代表 L2范数正则化， 同理，如果下标是1，则是 L1范数正则化。

1.2. 优化方法的数学表达式

机器学习算法使用损失函数的最终目的，是为了使用优化方法将偏差减到最小。优化方法通常使用梯度下降等现成算法，具体实现颇为复杂，但要用数学符号把意思表达出来却十分简单，一个是损失函数，另一个是最小化。

损失函数前面已经有现成的了，只要套一个最小化符号： $\min\limits_{w,b} ||\hat{y} - y||^2_2$

min 符号意为“求得最小”，正下方放了两个字母w和b，w和b正好分别表示线性方程的斜率和截距。

优化的方法很明显了，就是通过调节参数w和b，使得损失函数的表达式求得最小值： $||\hat{y} -y||^2_2$

1.3. 在Python中使用一元线性回归算法

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression


def regress():
    # 生成数据集
    x = np.linspace(0, 6, 40)
    y = 2 * x + 1

    # 给数据集添加一定的扰动，使之变得杂乱一点
    y = y + np.random.rand(40)

    # 将序列转为矩阵
    x = [[i] for i in x]
    y = [[i] for i in y]

    # 训练模型
    lr = LinearRegression()
    lr.fit(x, y)

    # 提供测试数据
    x_ = [[1], [2]]

    # 进行预测学习
    lr.predict(x_)

    # 法向量（由线性回归学习到的）
    k = lr.coef_
    # 截距（由线性回归学习到的）
    b = lr.intercept_
    # 线性函数（由线性回归学习到的）
    z = x * k + b
    print("法向量：", k)
    print("截距：", b)

    # 数据集绘图
    # 添加散点
    plt.scatter(x, y)
    # 添加学习到的线性函数
    plt.plot(x, z)
    plt.show()


if __name__ == "__main__":
    regress()

matplotlib 画出的图像如下：

线性回归模型在扰动中“学到”的线性函数图像

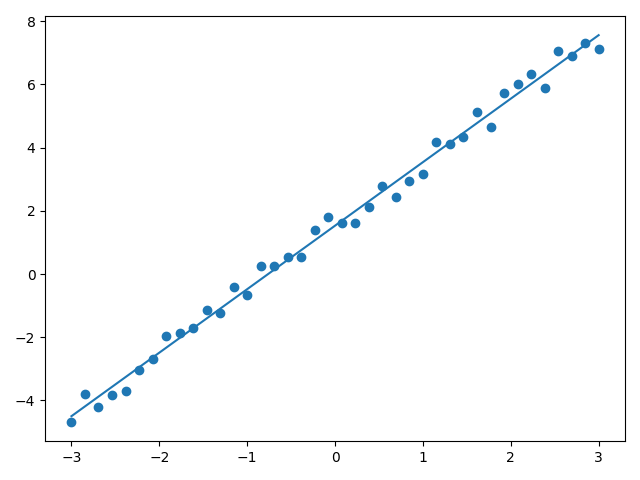
可以看出，加入随机扰动后，线性回归模型对法向量w的学习还是比较准确的，但对于截距项就出现了较大影响。

2. 多元线性回归分析

3. 线性回归的梯度下降模型

3.1. 在Python中使用线性回归梯度下降模型